Leibniz and the Idea of Universal Machine – Olga Pombo

Download in pdf: Leibniz and universal machine – Mana Platform

Abstract – After short considerations on the concept of machine and on the paradoxes of its articulation with men’s life, I will try to show how the leibnizian theory of symbolism anticipates the contemporary theses of the continuity man-machine and offers the fundamental basis for the idea of universal machine.

& 1. Machines

We know that the word machine comes from the Latin machina which, by its turn, comes from the Greek μαχανά and μηχανή, a derivation of μῆχος, meaning “means, expedient, remedy”. However, above this large, open etymological sense, Physics – as an inclusive, all-encompassing discipline as it has been up until the end of the XX century  – was able to impose a much more restricted and technical conception of machine as any device capable of changing the direction or the intensity of a force by means of some work.

However strict, this conception of machine gave rise to a much optimistic view of the value of machines in men’s life. From all the classical machines – from the Archimedean lever, pulley and screw (III century Ac), and the Ieron of Alexandria’s wind wheel and wedge (10–75 ac) – to Galileu’s inclined plane and Watt’s steam engine (1736-1819), machines were positively praised because they substitute human labor, they liberate mankind of hard activities, they improve the production of merchandises and they deeply increase the profit of bourgeoisie.

Diderot (1713 – 1784) is an eloquent example of this optimistic view. In his monumental Encyclopédie des Sciences, des Arts et des Métiers (1751), mechanical arts are highly valued by its utility to mankind. Because the Encyclopédie is at the service of people, it must be open not only to the sciences but also to the mechanical arts and labor activities of ignored artists and artisans who contribute for progress as much as the science men or the poets. As D’ Alembert writes in the Discours Préliminaire (1751), “the discovery of the compass was not less relevant to humanity than the explanation of that needle’s properties by Physics” (D’ Alembert, 1965: 56).

That valorization of mechanical arts and labor activities is the deep reason for Diderot’s detailed description of all kinds of machines, from the simplest to the most complicated ones[1]. In fact, in addition to discursive descriptions, Diderot provided remarkable impressed pictures showing in a much ostensive, didactic and theatrical way each represented machine[2]. First he presented a general view of the machine, usually together with horizontal or vertical cuts; later, the diverse elements of the whole mechanism; lastly, several layers of its internal organization and of its productive design[3].

Nonetheless, one hundred years later, views on machines begin to change. Optimism begins to give the place to a critical perspective towards machines. Stuart Mill, in his influential Principles of Political Economy (1849) did not hesitate to question the real value of machines for men’s life. As he states: “It is questionable if all the mechanical inventions yet made have lightened the day’s toil of any human being” (Mill, 1849: IV, 6.9). And Karl Marx (1818-1883), in the XV chapter of his outstanding Das Kapital (1867), precisely untitled Machinery and large scale industry, had no doubts to denounce machines as means for the production of the surplus-value: “The objective of machines is to make cheaper the merchandise, to diminish the part of labor which the worker needs for himself, and to enlarge the part of work which he gives for free to the capitalist” (Marx, 1867: IV, 15, 3).

The movement of English industrial workers who, in the beginning of the nineteen century, used to break at night the boss’s machines in which they have work during the day – the so called Luddism – was not just the first worker’s movement fighting for better work conditions. It was a protest against the substitution of human labor by machines, a sign (and a symbol) of the each day larger and insidious role played by machines in men’s life[4].

On the contrary, the last decades of the XIX century were happy times marked by the emergence of many beneficial machines able to extraordinarily enhance the living conditions of mankind and to facilitate the day life of millions of human beings[5]. That development became more and more exponential and prodigious during the XX century. But, at the same time, during that same XX century, we were confronted with the coming out of the most dreadful machines[6] of which resulted unexpected dangerous results.

Chaplin, in his masterpiece, Modern Times (1936), expressed this fear towards machines in strong poetic images, hard to forget.

Forced to be seated at a modern eating machine, he is still able to smile. But he cannot avoid us to weep by seeing him tragically lost and victim of the blind, metallic moving parts of that powerful machinery.

That is to say, the machines which Physics allowed us to construct have produced an enormous ambiguity. The XX century hesitates between the euphoric, apologetic delight about the constantly new technological progresses of more and more sophisticated and highly helpful machines, and the fear, the regret, the disappointment face to the inhuman, alienating, polluting nature of some harmful machines.

& 2. Universal Machines

It is in this very context that appears the Universal Machine. Precisely in the same moment Chaplin produces Modern Times (1936), the universal machine is designed in a concise article – On Computable Numbers – published by Turing (1912-1954) at the Proceedings of the London Mathematical Society (1936).

Apparently, it was just a brilliant article by a brilliant young mathematian of 24 years old.  But the fact is that such short article provided the central concept and the mathematical theory necessary for the construction of the computer, a machine able to change the face of the world and to radically transform what men think about men.

It is true that universal machine does not make it disappear the above mentioned ambiguity. On a certain sense, it makes it even more obvious. In fact, when, in 1996, exactly sixty years after Turing’s seminal article, Deep Blue triumphed over Kasparov, we all felt that this was not an innocent chess game. Something of high relevance had just happened[7].

What is necessary to realize is that universal machine is a new type of machine. It cannot be contained inside the definition we inherited from Physics. Universal machine is not just a device able to change the direction or intensity of a force by means of work. Universal machine is an intelligent, conceptual, cognitive machine. It is less an instrument, a tool, a resource, an artificial apparatus able to substitute human work and more a device which prolongs, complements, enlarges human activities and capacities. In fact, with the computer men’s relation to machines has decisively changed. A new theorization of the idea of machine begins to be imposed. Now, I believe, we need to think out the concept of machine without plunging neither in catastrophist pessimism nor in technological triumphalism. We require tranquility and backwards capacity for questioning machines in their origins, in their grounds, in their novelties and continuities, in their monstrous proliferation.  And we have to enlarge our conception of machine, to overcome the strict sense we inherited from Physics and to come across a much more distended idea of machine. We have to understand that among all the cultural artifacts produced by mankind, machines are extensions, expansion devices which do not only substitute but prolong, complement and extend our capacities.

& 3. Extended Mind

One of the most meaningful references is the celebrated article The Extended Mind published by Andy Clark and David J. Chalmers in 1998.

The more important points are precisely the claim for the enlargement of the concept of machine and its independence towards the concept of technology (aspirin is a technological product but the coup de point is a machine as well as the plow, the cart, the pencil, the notebook or the computer.

Two main theses are here present: 1) machines are not simply means to reach ends, mere tools or instruments which substitute human labor. They are extensions, expansions of our capacities of perception, memory and calculus. They are extrinsic devices; mundane, tangible procedures which prolong, amplify, enlarge, complement and extend our mental capacities; 2) cognitive machines (such as the pencil, the typewriter, the filofax or the computer) operate on basis of a language and of a writing.

Now, it is precisely in this moment that I would like to make a step back to Leibniz (1646-1716). I believe that our going-back capacity for questioning the primordial groundings of the idea of universal machine may be is worthwhile.

& 4. Leibniz

Leibniz was a theoretical thinker always committed with practical action. Further the design of extremely ambitious projects  such as the characteristica universalis[8], the encyclopedia universalis, the scientia generalis – too ambitious and innovative to be achieved – he has promoted great realizations such as academies, scientific journals or irenic institutions[9] and dedicated much of his time to invent functional solutions for technical problems such as the wind-driven propellers  for the extraction of silver and ore in the mines of Harz, water pumps and other hydraulic machines, lamps, submarines, portable watches of which he left detailed design[10].

We also know that Leibniz was one of the first who had the idea of a logical machine able to enhance human intellectual capabilities and make more easy, quick and rigorous the realization of calculus and invention. Since his De Arte Combinatoria of 1660, he conceives and develops a set of combinatorial, synthetic and inventive procedures on basis of what he calls since then the alphabet of human thoughts.[11] The idea was that the establishment of a combinatory apparatus which, further the demonstrative logics of Aristotle, would not be limited to the analysis of the truths already known but would make possible the discovery of new truths.

However, Leibniz is mentioned as a pioneer of the history of computer mostly by his invention of the Machina Arithmetica. Leibniz thought it out since 1671 but only in 1672 he advanced its construction after having been informed, during his stay in Paris, about a calculating machine previously invented by Pascal. Leibniz decided immediately to ameliorate Pascal machine, only able to add and subs cat. In 1673, Leibniz presented in the French Academy and in the Royal Society a wooden prototype of his arithmetic machine which had the ability, not only of adding and subtracting as the Pascalina did, but also of multiplying and dividing. Two years later, in 1675, he presented a metal prototype[12] to Arnauld e Huygens in the French Academy and, in 1676, made a full demonstration of his arithmetic machine again in the Royal Society.

Leibniz was committed to this project all along his life. In his De Progressione Dyadica (1679) he provides a full description of his arithmetic machine operating via binary arithmetic he had just discovered.[13] The machine was based on punctured devices whose holes would be open when corresponding to 1 and close when corresponding to 0, a surprisingly modern mechanism which was to be continuously developed up to the XX century.  Other detailed descriptions may be found in his Machina arithmetica in qua non aditio tantum et subtractio sed et multiplicatio nullo, divisio vero paene nullo animi labore peragantur (1685) and, much later, in his Brevis Descriptio Machinae Arithmeticae, cum Figura (1710).

It is true that, as many other of Leibniz projects, the arithmetical machine remained unfinished. However, Leibniz fundamental importance for the development of universal machines comes from his deep comprehension of their symbolic groundings, that is, from his theory of symbolism, close to the extended mind contemporary claims.

& 5. Lull, Hobbes and Leibniz

Leibniz work in this domain has two main roots[14].  The first root is Ramon Lull (1232-1315) whose Ars Magna   constitutes the remotest proposal of mechanization of logical procedures, a proposal which Leibniz knew well, stoutly criticizes and quotes since his De Arte Combinatoria (1660). Lull’s central idea is that it would be possible, by the combination of a set of simple terms, to establish all possible propositions and thus to discover all possible statements and demonstrate all possible truths to which human knowledge can aspire. For the accomplishment of this project, Lull proposes a set of categories, a system of notations, a finite number of syntactic rules and points to a complex system of combinatorial mechanical procedures of automatic application (a set of material circles, rotating in concentric movement of superposition in order to allow the combination of the symbols marked in their limits).

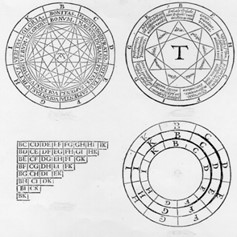
Leibniz criticizes the incompleteness and imprecise nature of Lull’s categories, the arbitrariness of the system of signs he has elected and the methodological solutions proposed by Lull. Instead, Leibniz proposes a much deeper analysis of the primitive terms, claims for a non-arbitrary system of signs and, by taking mathematics as the model, looks for submitting all human intellectual activity to calculatory processes.

The second main root of Leibniz theory of symbolism is Thomas Hobbes. For Hobbes (1588-1679), language is not a mere communication tool but above all a cognitive device. As Hobbes states in his treatise of Human Nature (1650): “it is by the very names that we are able to stabilize one representation” (V, § 4). We need words to fix our thoughts. We need words to think. We could not think without words. To think is to work out (to calculate) through words or, as Hobbes says in his masterpiece Leviathan (1651), “Reason is nothing but Reckoning (that is Adding and Subtracting) of Consequences of general names agreed upon, for the marking and signifying of our thoughts” (Leviathan: 11).

That is, only language provides the symbolic elements upon which the activity of calculus may be realised. And language is the sensible support for thought. It provides the material, signifying conditions required for the development of calculation. Hobbes is here giving a significant contribution to Leibniz who will fully adopt Hobbes’ cognitive conception of language. And indeed, Leibniz recognizes his heritage from Hobbes precisely in this point. As he states:

“Names are not only signs of my present thoughts for the others but notes of my previous thoughts to myself, as Thomas Hobbes has demonstrated” (our emphasis)[15].

But Leibniz will give an important step further. He will work out the cognitive conception of language formulated by Thomas Hobbes however building a new theory of symbolism which makes possible to explore a set of epistemic and heuristic consequences of which Hobbes never suspected. As Leibniz states:

 « When I think on one thousand or on a chiligone, I do it without contemplating those ideas, without putting me in the need of thinking what it is 10 and 100, because I suppose I know it and I do not have the need of conceiving it at this moment».[16]

For Hobbes, we need words to think what we are able to think. For Leibniz, we need words to think what we are not able to think (the chiligone, great numbers). For Hobbes, only with language we are able to think. For Leibniz, with language we are able to think what we will never be able to think otherwise.

& 6. Leibniz’ theory of blind though

That is the main point of Leibniz’s celebrated theory of cogitation caecae, one of the greatest discoveries of Leibniz’s philosophy of language.[17]

« In general, and above all if the analysis is too long, we do not simultaneously see all the nature of the thing but we use signs instead of the things (…) I call this knowledge as blind or symbolic; we make use of it in algebra and arithmetic’s and in almost all domains“ (our emphasis) [18]

Men cannot think simultaneous and constantly the greatest part of his ideas. However men has the possibility of thinking those ideas through the symbols which represent them, that is, men has the possibility of investing the symbols with a much larger meaning than the one he has in the moment. As Leibniz said early in the De Arte (1660):

« Nobody may calculate, especially with great numbers, without names or numerical signs since it would be necessary to distinctively imagine, instead of the number, all the unities in it contained. Who could distinctively imagine all the unities included in 1.000.000.000.000 unless having the age of Mathusalem?”[19]

Against Descartes who claimed the need of seeing it all with the yeas of soul, who grounded mathematics in the evidence of its propositions, Leibniz accepts to go on progressing through a though that is blind, that is, he aims to progress without seeing nothing.  Just with the external, material, sensible support of symbolism.

« The true method must provide us with a Filum Ariadnes, that is to say a kind of sensitive and rude means that guides mind in the same way as lines drawn in geometry and as the form of operations  that are prescribed to apprentices in arithmetic”.[20] (our emphasis)

The true method does not entail, as in Descartes, the confidence in the intuitive rightness of natural light. The true method requires the construction of an artificial symbolic device able to prolong, expand, extend natural reason.  It is precisely in the systematic recovery to symbolism that, according to Leibniz, rests the secret of mathematics. They are more than a chain of intuitive reasons, as Descartes wanted. They are a machine operating with symbols, they bring with them their own procedures of control and confirmation.The following text of the Preface à la Science Générale (1677) is eloquent:

“The reason why the art of demonstrating has been until now found only in mathematics (…) is this: Mathematics carries its own test with it. For when I am presented with a false theorem, I do not need to examine or even to know the demonstration, since I shall discover its falsity a posteriori by means of an easy experiment that is, by a calculation, costing no more than paper and ink”. (our emphasis) [21]

Thought operations may – and must – be realized directly on the symbols without being necessary to go back to the ideas they are supposed to substitute. That is the secret: to affix reasoning to the manipulation of the symbols, “to oblige reasoning to leave visible traces on the paper”[22].

“(…) so, we may make sensible the analysis of thought and we may guide it, as by a mechanical filum”[23](our emphasis)

This is exactly what Turing did. He fully realized that computing is based on external linguistic encodings of human mental states, that is, well defined mathematical signs connected by precise operational rules. As he stressed:

 “Computing is normally done by writing certain symbols on paper (…) The behavior of the computer at any moment is determined by the symbols which he is observing” (Turing, 1936: 249-250

&  7. Final remarks

Here the four points I would like to reach with these quick questioning on the concept of machine:

1) Machines are extensions, expansion devices which do not only substitute but prolong, complement and extend our capacities

2) There is continuity between the most elementary gestures of cultural artifact production and the most sophisticated machines which surround us.

3) Neither catastrophist pessimism nor a technological triumphalism; neither unlearned rage nor erudite nostalgia.

4) We may became amazed, overwhelmed, but we do not need to became afraid, scared.

[1] This is the case of the celebrated entrance “Bas” in which Diderot follows the expertise of M. Barrat who taught him the functioning procedures of the fantastic machine of making socks. For further developments, cf. Pombo (2006: 194-251).

[2] We could say that the Encyclopédie is, in itself, a machine, a vast procedure aiming to grasp, to penetrate, to decipher, to represent and to systematize all the secrets of Nature and Arts. All may be seen, open, shown, exposed to light of reason, both the interior of factories, ateliers and laboratories to the most antique agriculture and manufacture devices, the geological deepness of earth, of mines, of bodies, of machines (Cf. ibid).

[3] Corresponding to a period of developed manufacture economy, anterior to the introduction of steam engine, the Encyclopédie conceives technical labor, not anymore in its theological meaning, as divine punishment, not yet in its romantic dimension, as getaway of the agriculture tasks by which men may only be in harmony towards Nature, but as a form of progressive humanization of world, as exteriorization of knowledge, practical extension allowing to take off from science all its technical utility (Cf. ibid).

[4] The name of that movement comes from the worker Ned Ludd, leader of the pressure group who used to break at night the boss’s machines in which they have work during the day. After the night assault to the William Cartwright’s manufactory, in April 1812, a major process against luddites was put forward. Seventy four workers were accused of having attempt against the factory, thirteen were condemned to dead and two were deported to colonies. For further developments and actual impact, cf. Sale (1995).

[5] Namely, the telephone (1878), the automobile (1886), the photographic machine (1888), the cinematograph (1895) or the radiography (1895).

[6] Such as the fighting cars of the first world war, the ballistic missiles of 1938, the atomic bomb of 1945, the nuclear reactors of 1956, the drones first used in Balkan, Afghanistan and Iraq wars.

[7] Kasparov’s words at the end of the game are filled by such awareness: he had been the last human to win chess championship.

[8] The Characteristica Universalis was in fact thought out as a machine similar to a microscope or a telescope. As Leibniz writes:  “Humanum Organi genus novum, plus  multo mentis potentiam aucturum, quam  vitra optica oculos juverunt, tantoque superius Microscopiis aut Telescopiis  quanto praestantior est ratio visu” (Leibniz, GP 7: 187).

[9] Leibniz aimed to create national scientific societies in Dresden, Saint Petersburg, Vienna, and Berlin. Of those such only the Berlin Academy of Sciences, was indeed created in 1700 by Leibniz who designed its first statutes and served as its first President up until his dead in 1716. On Leibniz’s projects for scientific societies, see Couturat (1901: 501-528, IV Appendices untitled «Leibniz fondateur d’Académies» ). On Leibniz irenic project and many attempts of unifying Christianity, cf.  Baruzzi (1907).

[10] Many scholars have underlined the practical activity which runs parallel to Leibniz theoretical thinking. See the case of Elster (1975) or Manuel Sanchez Rodriguez and Sergio Rodero Cilleros (eds)(2010).

[11] Cf. Leibniz (GP 4: 72-73). For further developments on this Leibnizian project, cf. Pombo (1987: 86-91 and 171-174).

[12] Leibniz ordered manufacturing probably ten other prototypes of his arithmetic machine of which two are still conserved (one at the Landesbibliothek, Hannover, and other at the Deutsches Museum, München).

[13] In a memory written late, in 1703, untitled Explication de l’arithmétique binaire qui se sert des seules charactères 0 et 1, avec des remarques sur son utilité, et sur ce qu’elle le sens das anciennes figu­res chinoises de FoHi (Leibniz, GM 7: 223-7), Leibniz explains in detail his discovery of binary system and its analogy with the FoHi hexagrams which the Jesuit Bouvet have sent him from China.

[14] In another paper, I claimed, not of two but of three roots of Leibniz’s computational conception of reason, the third being the XVII century projects of philosophical language. Cf. Pombo (2010).

[15] «Verba enim non tantum signa sunt cogitationis meae praensentis ad alios, sed et notae cogitationis meae praeteritae ad me ipsum, ut demonstravit Thomas Hobbes» (Leibniz, Ak. VI, 1. 278).

[16] « Lors que je pense à mille ou à un chiligone, je le fais sans en contempler l’idée, sans me mettre en peine de penser ce que c’est que 10 et 100, parce que je suppose de le savoir et ne dois pas d’avoir besoin à present de m’arrester à le concevoir » (Leibniz, GP 4: 450‑451)

[17] Which we have studied in Pombo (1998).

[18] “Plerumque autem, praesertim in Analysi longiore, non totam simul naturam rei intuemur, sed rerum loco signis utimur, quorum solemus praetermittere, scientes aut credentes nos eam habere in potestate (…) qualem cogitationem caecam vel symbolicam appellare soleo, qua et in Algebra et in Arithmetica utimur, imo fere ubique» (Leibniz, GP 4: 423)

[19] « Quemad modum enim nemo computare posset, praesatim numeros ingentes, sine nominibus vel signis numeralibus, loco numeri enim deberet sibi distincte imaginari omnes in eo comprehensas unitates. Quis autem nisi tempore aetatis Methusalae imaginabitur sibi distincte unitates quae sunt in 1.000.000.000.000 et si posset tamen progrediendum priorum obliviscertur” (Ak 6.2: 481).

[20] « La veritable méthode nous doit fournir un Filum Ariadnes, c’est à dire, un certain moyen sensible et grossier, qui conduise l’esprit, comme sont les lignes tracés en geométrie et les formes des opérations qu’on prescrit aux apprentifs en Arithmetique» (Leibniz, GP 7: 22). (our emphasis).

[21] « Or la raison pour quoy l’art de démonstrer ne se trouve jusqu’ici que dans les mathématiques (…) est que les mathématiques portent leur épreuve avec elles: car quand on me présente un théorème faux, je n’ay pas besoin d’en examiner ny même d’en sçavoir la démonstration, puisque j’en découvriray la fausseté à posteriori par une expérience aisée, qui ne coîte rien que de l’encre et du papier» (Leibniz, C: 154)(our emphasis).

[22] As Leibniz says : «le secret est de fixer le raisonnement, et de l’obliger à laisser comme des traces visibles sur le papier, pour estre examiné à loisir » (Leibniz, C : 99)

[23]“(…)hinc analysin cogitationum possumus sensibilem reddere, et velut quodam filo mechanico dirigere» (Leibniz, C: 351). Leibniz also uses filum cogitandi (Leibniz, C: 420) and filum meditandi (Leibniz, GP 7: 14)(our emphasis).

References:

BARUZI, Jean (1907), Leibniz et l’ Organization Religieuse de la Terre, Paris: Felix Alcan.

CLARK, Andy and CHALMERS, David J. (1998), “The Extended Mind”, Analysis, 58: 10-23.

COUTURAT, Louis (1961),  La Logique de Leibniz d’après des Documents Inédits. Hildesheim: Georg Olms Verlag.

D’ALEMBERT, Jean le Rond  (1751), Discours Préliminaire de l’Encyclopédie, Paris: Gonthier (1965).

ELSTER, Jon (1975), Leibniz et la Formation de l’Esprit Capitaliste,  Paris: Aubier Montaigne.

HOBBES, Thomas (1651), Leviathan, edited by C. B. Macpherson, London: Penguin Books, Pelican Classics (1968).

HOBBES, Thomas (1650), Human Nature or the Fundamental Elements of Policy, V, § 1, in The Elements of Law Natural and Politic, ed. F. Tönies, London: Frankcass (1969).

SALE, Kirkpatrick (1995), Rebels against the Future: the Luddites and their War on the Industrial Revolution: Lessons for the Computer Age, London:  Basic Books.

LEIBNIZ, Gottfried Wilhelm Leibniz Samtliche Schrifften und Briefe, Akademie der Wissenschaften zu Berlin, Reihe I ­– VI, Darmstadt: Reichl (1923 segs).  [Ak] 

LEIBNIZ, Opuscules et Fragments Inédits de Leibniz. Extraits des Manuscrits de la Bibliothèque Royale de Hannover par Louis Couturat. Paris: Alcan, 1903. [C]

LEIBNIZ, Gottfried Wilhelm Leibniz. Mathematische Schriften, Hrsg. v. Carl Immanuel Gerhardt. 1­‑7. Hildesheim: Olms, 1962.  [GM]

LEIBNIZ, Die Philosophischen Schriften von Gottfried Wilhelm Leibniz. Hrsg v. Carl Immanuel Gerhardt. 1­‑7. Hildesheim: Olms, 1960.  [GP]

LLULL, Ramón (1308), Ars Brevis (translation, introduction and notes by Armand Llinarès), Paris: Cerf (1991).

MANUEL SANCHEZ RODRIGUEZ and SERGIO RODERO CILLEROS (2010), Leibniz en la Filosofia Y la Ciencia Modernas, Granada: Comares.

MARX, Karl (1867), Capital (English translation by Bem Fowkes), London: Penguim Classics (1976).

MILL, Stuart (1849), Principles of Political Economy with some of their Applications to Social Philosophy, London: Longmans (1909).

POMBO, Olga (1987), Leibniz and the Problem of a Universal Language, Münster: Nodus PubliKationen.

POMBO, Olga (1985), “Linguagem e Verdade em Hobbes”, Filosofia nº 1: 45-61.

POMBO, Olga (1998),  « La Théorie Leibnizienne de la Pensée Aveugle en tant que Perspective sur quelques-unes des Apories Linguistiques de la Modernité », Cahiers Ferdinand Saussure, 51: 63-75.

POMBO, Olga, (2006), “Para uma História da Ideia de Enciclopédia. Alguns Exemplos”, in O. Pombo; A. Guerreiro e A. Franco Alexandre (Eds.), Enciclopédia e Hipertexto, Lisboa: Editora Duarte Reis, pp. 194-251.

POMBO, Olga (2010), “Three Roots for Leibniz’s Contribution to the Computational Conception of Reason”, in F. Ferreira; B. Löwe; E. Mayordomo; L. M. Gomes (Eds.), Programs, Proofs, Processes. 6th Conference on Computability in Europe, CiE 2010, Berlin: Springer, pp. 352-361.

TURING (1936), “On Computable Numbers”, Proceedings of the London Mathematical Society, 12: 230-265.