لويس كارول هو الاسم المستعار للكاتب الإنجليزي تشارلز لوتويدج دودسن (1832 – 1898) الذي أعاد إحياء شخصيات المحارب أخيل (Achilles) والسلحفاة التي اشتهرت قديمًا مع الفيلسوف اليوناني زينون الإيلي (490 ق.م – 430 ق.م). رواية زينون »أخيل والسلحفاة« هي واحدة من مجموعة روايات تُعرَف بإسم مفارقات زينون (Zeno’s paradoxes)، مفادها أنّ الحركة مستحيلة أو أنها عبارةٌ عن وهمٍ لأنّ أخيل لن يستطيع ربح السباق مع سلحفاةٍ بدأت بالسير قبله. لويس كارول، وهو مؤلّف رواية »أليس في بلاد العجائب« (1865)، كَتَبَ مقالًا بعنوان »ماذا قالت السلحفاة لأخيل« (1895)، وهي روايةٌ قصيرةٌ تتضمّن حديثًا يجري بين السلحفاة وأخيل للتعبير عن مفارقةٍ مغايرةٍ عن مفارقة زينون، قام بالتعليق عليها العديد من الفلاسفة وأهمّهم برتراند راسل. السلحفاة تعترف بخسارتها السباق عمليًّا رغم أنّ زينون أوضح نظريًّا أنّ هذه الخسارة لا يمكن أن تحصل. ألمحت السلحفاة إلى أنّ سبب الخسارة هو التناقص المستمر للمسافات المتلاحقة التي تفصلها عن أخيل في السباق، ثم سألت أخيل »لكن ماذا لو كانت تتزايد باستمرار؟« (Carroll 691) وقامت ببناء تسلسلٍ لانهائيٍّ من الجُمَل التي يتزايد فيها عدد الكلمات باستمرارٍ لمنعنا من الوصول إلى استنتاجٍ بديهيٍّ في علم المنطق. تحديدًا، انتقدت السلحفاة استنتاج إقليدس (Euclid) بأنّ مسافتان تسويان بعضهما إذا كان كلٌّ منهما يساوي مسافةً ثالثةً. إقليدس كان يطبّق هذا الاستنتاج المنطقي على أضلاع المثلث (the triangle sides)، مُستنتجًا أنّ ضلعين يكونان متساويين إذا كان كلٌّ منهما متساوٍ مع الضلع الثالث، وهذا للحصول على مثلثٍ متساوي الأضلاع (equilateral triangle). لويس كارول، مستخدمًا السلحفاة في الرواية، يؤكّد بأنه لا يمكننا منطقيًّا إتمام هذا الاستنتاج. في هذا المقال، سوف أطرح مفارقة زينون محدّدًا خلفيّاتها، ثم أوضّح مفارقة لويس كارول بعد عرض استنتاج إقليدس الذي تمّ نقده. وأخيرًا، بعد عرض تعليقات وحلول بعض الفلاسفة، سوف أقدّم حلًّا لهذه المفارقة معتمدًا على ما قدّمه الفيلسوف البريطاني غلبرت رايل (1900 – 1976) في مقالِهِ «معرفة كيف ومعرفة ذلك» (Knowing how and Knowing that) عام 1946 حيث يوضّح الفرق بين معرفتنا لفكرةٍ معينةٍ ومعرفتنا لقاعدةٍ تعلّمنا كيف ننتقل من فكرةٍ لأخرى.
مفارقة زينون «أخيل والسلحفاة»
تأثر زينون الإيلي بالفيلسوف بارمينيدس (540 ق.م – 480 ق.م) الذي يجادل بأنّ كلّ ما تتلقّاه حواسنا من تغييراتٍ في العالم وكثرةٍ، ما هو مغايرٌ لوِحدة الأشياء، هي مجرد أوهامٍ. ركّز زينون عملهُ الفلسفيّ على رفض التغيُّر لدعم نظرية بارمينيدس، وتحديدًا على التغيُّر الذي يصدر عن الكائنات الحية، أي الحركة. مع العلم أنّ هذه النظرة الفلسفية كانت تتواجه مع نظرة هرقليطس (535 ق. م – 470 ق. م) صاحب مقولة «لا يمكنك أبدًا أن تخطو في نفس النهر مرتين»، ما معناه أن العالم في تغيُّرٍ دائمٍ. يروي زينون في مفارقة أخيل والسلحفاة عن المحارب أخيل بأنه في سباقٍ على قدميه مع السلحفاة. يسمح أخيل للسلحفاة ببداية السباق أن تكون متقدمةً عليه بمسافة مئة متر، على سبيل المثال. فلنفترض أنّ كلّ متسابقٍ يبدأ في الجري بسرعةٍ ثابتةٍ، حيث تكون سرعة أخيل أكبر من سرعة السلحفاة طبعًا. بعد مرور بعض الوقت، سيكون أخيل قد ركض مئة متر ليصل إلى نقطة انطلاق السلحفاة، النقطة الأولى. خلال هذا الوقت، تكون السلحفاة قد ركضت لمسافةٍ أقصر بكثيرٍ، لنَقُل مترين. والآن، سوف يتوجّب على أخيل ركض تلك المسافة للوصول للنقطة الثانية للسلحفاة، وفي ذلك الوقت ستكون السلحفاة قد تقدمت أكثر بمسافة أقل من مترين لتصل إلى نقطةٍ ثالثةٍ. وعن جديد، سوف يكون أخيل بحاجةٍ للمزيد من الوقت للوصول إلى هذه النقطة الثالثة، بينما تتحرك السلحفاة للأمام. وهكذا، كلّما وصل أخيل إلى نقطةٍ ما كانت فيها السلحفاة، لا يزال أمامه بعض المسافة ليقطعها قبل أن يتمكّن من الوصول إلى نقطة تواجد السلحفاة. وهذا نظريًا سيتكرر إلى ما لا نهاية من دون أن يصل أخيل إلى السلحفاة ويربح السباق، وهذا يعود إلى أنّ مهما كانت المسافة قصيرة، فهي قابلةٌ للتجزئة.
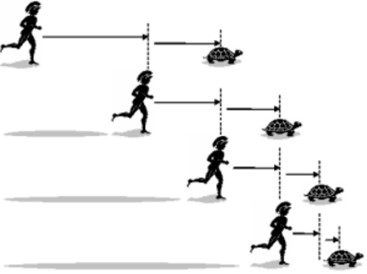
هناك طريقةٌ أخرى لعرض هذه المفارقة، وهي على الشكل التالي: لكي يتحرّك جسمٌ معينٌ إلى نقطة ‘أ’، لا بدّ له قبل ذلك أن يصل إلى النقطة ‘ب’، وهي منتصف طريقه إلى ‘أ’، ولكي يصل إلى ‘ب’ يجب أن يصل أوّلًا إلى النقطة ‘ج’ التي هي منتصف طريقه إلى ‘ب’، وهكذا إلى ما لا نهاية تنقسم كل مسافةٍ إلى نصفها. وبما أنّ هذه السلسلة من الخطوات المطلوبة لا نهاية لها، فهي تتطلّب قدرًا من الوقت لا نهاية له للقيام بها. لذلك السبب، يستنتج زينون أنّ تحرّك أيّ جسمٍ إلى أيّة نقطةٍ في زمنٍ محدّدٍ هو أمرٌ مستحيلٌ نظريًّا.
إنّ الخطأ الرياضيّاتيّ هو في القول إنّ أخيل لن يصل أبدًا للسلحفاة، لأن التحليل الحديث في الرياضيات يؤكّد أنّ سلسلةً لانهائيةً من الأرقام الموجبة (positive) يمكن أن تتقارب مع نتيجةٍ محدودةٍ، أي أنّ مجموعًا (sum) لانهائيًّا من المسافات يمكن أن يعطي جوابًا نهائيًا (finite). فيمكننا معالجة الموضوع نظريًا من خلال ترجمته إلى متسلسلةٍ هندسيةٍ (geometric series) ونثبت أنها متسلسلةٌ متقاربةٌ (convergent series). لن أدخل في إثباتٍ رياضيّاتيٍّ مفصّلٍ، لكن سوف أعرض مثالًا يعبّر عن الفكرة الأساسية لحلّ المفارقة. إذا كانت سرعة أخيل عشرة أمتار بالثانية وسرعة خمسة أمتار بالثانية للسلحفاة التي تتقدم بمقدار مئة متر عن أخيل، تستغرق الخطوة الأولى 10 ثوانٍ، ثم 5 ثوانٍ للخطوة التالية، إلخ. إذا كنا نريد معرفة بعد كم من الوقت سوف يلتقي أخيل بالسلحفاة، علينا أن نقيم مجموع مدّة الخطوات التي تكون في كلّ مرّة بقدر نصف السابقة، فنحصل على السلسلة التالية اللانهائية منها: 10 + 5 + 2,5 + 1,25 + … وأخيرًا، الجواب الدقيق هو: 20 ثانية، كونه مجموعٌ لمتسلسلةٍ هندسيةٍ فيها المعامل (coefficient) يساوي 0,5. وهناك طريقةٌ أسهل تكون من خلال رسم خطّين مستقيمين في نظامٍ إحداثيٍّ ديكارتيّ (Cartesian coordinate system) يمثّل كلٌّ منهما مسار أحد المتسابقين، وعندما يلتقي الخطّان المستقيمان في نقطةٍ معينةٍ، هذه النقطة تمثّل التقاء أخيل بالسلحفاة وتخطّيها في السباق.
جديرٌ بالذكر عمل الفيلسوف هنري برغسون (1859 – 1941) في عدّة كتاباتٍ له في التمييز بين الزمن الداخلي الذاتي (duration) والزمن الخارجي الموضوعي (time) الذي يتجزَّأ إلى ساعاتٍ ودقائقٍ وثوانٍ، حيث يرتبط مفهوم المسافة بالزمن الموضوعي والحركة بالزمن الذاتي. وبالتالي، يمكن اعتبار خطأ زينون الأساسي في الفلسفة هو عدم التمييز بين المسافة التي يمكن تجزئتها والحركة التي لا يمكن تجزئتها. أمّا في رواية لويس كارول، تأخذ السلحفاة المسألة بطريقةٍ عمليّةٍ وتقول بإنّه يمكن لأخيل أن يسبقها بما أنّ المسافات في انحدارٍ مستمرٍّ، وهذا ما يجعل المتسلسلة متقاربةً (convergent). ثم تُلفت السلحفاة نظر أخيل إلى أنّ المسألة سوف تتغيّر إذا كانت المسافات إلى ارتفاعٍ مستمرٍّ، لأنّ هذا ما سيجعل المتسلسلة متباعدةً (divergent). ففي حال كانت السلحفاة أسرع من أخيل ومتقدّمةٌ عليه من بداية السباق، سوف تقطع مسافةً أكبر من التي يقطعها أخيل في وقتٍ معيّنٍ، ولن يستطيع أن يربح السباق. وبما أنّ هذه الفكرة بديهيّةٌ وليس هناك اعتراضًا عليها، انتقلت السلحفاة إلى مسألةٍ بديهيّةٍ في علم المنطق، يُظنّ عادةً أنّ أمرها ينقضي بخطواتٍ قليلةٍ، لكنّ السلحفاة سوف تثبت أنّ الأمر في حقيقته يؤدّي إلى عددٍ لامتناهٍ من الخطوات كلّ واحدةٍ منها أكبر من التي تسبقها. حسب تعبير السلحفاة لأخيل، «حسنًا الآن، هل تود أن تسمع عن سباق، يتخيّل معظم الناس أنه يمكنهم الوصول إلى نهايته بخطوتين أو ثلاث خطواتٍ، في حين أنه يتكوّن حقًا من عددٍ لانهائيٍّ من الخطوات، كلّ واحدةٍ أطول من السابقة؟» (Carroll, 691)
إقليدس
«حسنًا، الآن، دعنا نأخذ القليل من الحُجّة في تلك القضية (proposition) الأولى (لإقليدس )- خطوتان فقط، والاستنتاج المستخلص منهما. لطفًا أدخلها في دفتر الملاحظات الخاص بك» (Carroll, 691)، تقول السلحفاة لأخيل. يمكننا رؤية القضية الأولى المقصودة في هذه الصورة (Euclid, 8):
إنّ هدف القضية الأولى هو رسم مثلثًا متساوي الأضلاع انطلاقًا من قطعةٍ مستقيمةٍ، أي خطٍّ مستقيمٍ يمتدّ بين نقطتين محددتين. لكنّ السلحفاة تهتم فقط بقسمٍ واحدٍ من القضية، وهو كيف يستنتج إقليدس أن ضلعا المثلث يساويان بعضهما كونهما متساويين مع الضلع الثالث. لكي يصل إلى هذه النتيجة، يستعمل إقليدس أولًا النظرية الأولى من «النظريّات العامّة» (common notions) على حدّ تعبيره، وهي «الأشياء التي تساوي الشيء ذاته تتساوى أيضًا مع بعضها بعضًا» (Euclid، 7). ثم يوجد ضلعان في هذا المثلث يساوي كلٌّ منهما الضلع الثالث، ويستنتج من هاتين الفكرتين أنّ الضلعين متساويان. ولكي يكون الأمر واضحًا، طلبت السلحفاة من أخيل أن يكتب الاستنتاج على النحو التالي:
الفرضيات[1] (Hypotheses):
(أ): الأشياء التي تساوي الشيء ذاته تتساوى أيضًا مع بعضها بعضًا
(ب): ضلعا هذا المثلث هما شيئان مساويان لشيءٍ ثالثٍ
النتيجة (Conclusion):
(ي): ضلعا هذا المثلث متساويان
هذا الاستنتاج، الذي هو تحديدًا استنباط (deductive reasoning)، ينطلق من الفرضيتين (أ) و(ب) اللتان تكفيان بالنسبة لإقليدس للوصول إلى النتيجة (ي). لكن، سنرى في القسم التالي من المقال كيف ينقده لويس كارول معتبرًا الموضوع أكثر تعقيدًا من الاستعمال البديهي الذي قدّمه إقليدس وكثرٌ غيره من علماء الرياضيات والمنطق والفلاسفة، وطبعًا جميع الناس عامةً لأنّ هذا الاستنباط يُستعمل في حياتنا اليومية بشكلٍ بديهيٍّ.
التسلسل اللانهائي
تسأل السلحفاة أخيل ما إذا كانت النتيجة تَصدُر منطقيًّا عن الفرضيتين، ويؤكد أخيل ذلك بوضوح. ثم تسأله عمّا إذا كان من الممكن وجود قارئٍ لإقليدس يقبل أنّ الحُجّة صحيحةٌ كتسلسلٍ منطقيٍّ لكنه يرفض أن تكون الفرضيات (أ) و(ب) صادقةٌ، أي أنها كاذبةٌ. أخيل يُقِرّ بأنّ مثل هذا القارئ قد يكون موجودًا، فمن الممكن لشخصٍ ما أن يعتقد أنّ الفرضيتين ليستا صادقتين، ولكن في حال افترض أنها كذلك فهو يقبل بالنتيجة (ي) كنتيجةٍ ضروريةٍ للفرضيتين عبر تسلسلٍ منطقيٍّ. ثم تسأل السلحفاة أخيل ما إذا كان من الممكن وجود نوعٍ ثانٍ من القرّاء، كشخصٍ يقبل أنّ الفرضيتين (أ) و(ب) صادقتان، لكنه يرفض وجوب استنتاج أنّ القضية (ي) صادقةٌ انطلاقًا من أنّ الفرضيتين (أ) و(ب) صادقتان. أي أنه يقبل صحّة الفرضيّات ويرفض الحُجّة بذاتها أن تكون صحيحةً منطقيًّا لاستنتاج القضية (ي). يوافق أخيل بأنّ هذا النوع الثاني من القرّاء قد يكون موجودًا أيضًا. تطلب السلحفاة، إذًا، من أخيل أن يتعامل معها كقارئٍ من هذا النوع الثاني، ويجب على أخيل الآن إجبار السلحفاة منطقيًا على قبول أنّ القضية (ي) يجب أن تكون صادقةً.
إذًا، السلحفاة الآن تعتبر أنّ الفرضيتين (أ) و(ب) صادقتان لكنّ القضية الافتراضية (hypothetical proposition) القائلة «إذا كانت (أ) صادقةٌ و(ب) صادقةٌ، فإذًا (ي) يجب أن تكون صادقةً» ليست صادقةً بالنسبة لها. وحين طالبها أخيل بالقبول بها كافتراضيةٍ صادقةٍ، كان جوابها إيجابيًا لكن بشرط أن يكتبها بجانب الفرضيات، تحديدًا بين (ب) و(ي). لذلك، دوَّن أخيل التالي:
الفرضيات:
(أ): الأشياء التي تساوي الشيء ذاته تتساوى أيضًا مع بعضها بعضًا
(ب): ضلعا هذا المثلث هما شيئان مساويان لشيءٍ ثالثٍ
(ج): إذا كانت (أ) صادقةٌ و(ب) صادقةٌ، فإذًا (ي) يجب أن تكون صادقةً
النتيجة:
(ي): ضلعا هذا المثلث متساويان
توقّعَ أخيل أن تعترف السلحفاة بأنّ الحُجّة أصبحت مقنعةً منطقيًا بما أنها تقبل الثلاث فرضيات بأنها صادقةٌ. فهي منذ البداية اعتبرت (أ) صادقةٌ و(ب) صادقةٌ، والآن، بعد تدوين الافتراضية (ج) بجانبهم قَبِلت بها كقضيةٍ صادقةٍ. فالسلحفاة وعدت أخيل بأنها ستقتنع بحقيقة (ج) بمجرد تدوينها كفرضيةٍ، أي بين مقدمات الحُجّة. لكنها تُفاجِئ أخيل وتُعلِن عن جديد بأنها غير مقتنعةٍ باستنتاج (ي) رغم قبولها بحقيقة (أ)، (ب)، و(ج). استغرب أخيل رفضها للحُجّة قائلًا «إذا كان (أ) و(ب) و(ج) صادقين، فإذًا يجب أن تكون (ي) صادقةً». وكان جواب السلحفاة بأنّ ما قاله أخيل هو مجرد جملةٌ افتراضيةٌ ثانيةٌ، تشبه (ج) ولكن أطول منها لأنها تتضمّنها. لذلك السبب، طَلَبت مجدّدًا من أخيل وضعها بجانب الفرضيات الأخرى وإلّا لن تقبلها كحقيقةٍ، ممّا اضطُرّ أخيل أن يعدّل الحُجّة لتصبح كالتالي:
الفرضيات:
(أ): الأشياء التي تساوي الشيء ذاته تتساوى أيضًا مع بعضها بعضًا
(ب): ضلعا هذا المثلث هما شيئان مساويان لشيءٍ ثالثٍ
(ج): إذا كانت (أ) و(ب) صادقتين، فإذًا (ي) يجب أن تكون صادقةً
(د): إذا كان (أ) و(ب) و(ج) صادقين، فإذًا يجب أن تكون (ي) صادقةً
النتيجة:
(ي): ضلعا هذا المثلث متساويان
ثم طالبها أخيل أن تقبل بحقيقة (ي) الآن بعدما قبلت بحقيقة (أ) و(ب) و(ج) و(د). فإذا كانت الفرضيات الأربعة صادقةٌ، فيجب أن تكون (ي) صادقةً. ما دفعها من جديد، للقبول بهذه الافتراضية الأخيرة، المطالبة بتدوينها كفرضيةٍ خامسةٍ، لتصبح الحُجّة:
الفرضيات:
(أ): الأشياء التي تساوي الشيء ذاته تتساوى أيضًا مع بعضها بعضًا
(ب): ضلعا هذا المثلث هما شيئان مساويان لشيءٍ ثالثٍ
(ج): إذا كانت (أ) و(ب) صادقتين، فإذًا (ي) يجب أن تكون صادقةً
(د): إذا كان (أ) و(ب) و(ج) صادقين، فإذًا يجب أن تكون (ي) صادقةً
(ه): إذا كان (أ) و(ب) و(ج) و(د) صادقين، فإذًا يجب أن تكون (ي) صادقةً
النتيجة:
(ي): ضلعا هذا المثلث متساويان
وهكذا، يمكن المتابعة إلى ما لا نهاية، في كلّ خطوةٍ مع فرضيةٍ جديدةٍ تكون أطول من السابقة لها. لذلك، لن ينتهي الجدال أبدًا ولن يستطيع أخيل إقناع السلحفاة بأنّ (ي) صادقةٌ.
تعليقات بعض الفلاسفة
إنّ خطورة هذه المفارقة كامنةٌ في عدم قدرتنا على برهنة أيّ قضيةٍ منطقيًا. الاستعانة بالطريقة التجريبية لبرهنة استنتاج إقليدس الذي نقده لويس كارول هو أمرٌ مطروحٌ، لكن على أغلب الظّن أنّ الأخير أصرّ على معالجة الموضوع منطقيًا من دون اللجوء إلى التجربة بهدف نقد علم المنطق من أساسه. لذا، يمكن القول إنّ لويس كارول أراد التأكيد بأنّ علم المنطق لا يمكنه برهنة فرضيّاته، ممّا يدفع إلى إعادة النظر في تعريف علم المنطق وتحديد نظامه.
إنّ نظرة برتراند راسل (1872 – 1970) لعلم المنطق شبيهةٌ بنظرته للرياضيات، كلاهما يتضمّن مبادئٍ لا يمكن برهنتها (indemonstrable principles)، وفي حال رفضناها لا يمكننا برهنة أي شيءٍ آخر (Russell, 15). كما أنّ مشروعه الكبير وغير المكتمل في هذا المجال كان إعادة بناء الرياضيات على علم المنطق، لاعتبار المنطق كأساسٍ للرياضيات. الفكرة الأولى الأساسية لبرتراند راسل فيما يخصّ مفارقة لويس كارول مباشرةً، هي أنّ القضية (ج) القائلة «إذا كانت (أ) و(ب) صادقتين، فإذًا (ي) يجب أن تكون صادقةً»، هي قاعدةٌ استدلاليّةٌ (rule of inference). وفقًا لهذا النوع من القواعد، يمكننا أن نقوم باستنتاجٍ فوريٍّ من مقدماتٍ معينةٍ، بحيث يتم تعريف البرهان على أنه سلسلةٌ من الفرضيات التي تكون إمّا بديهيّات (axioms) أو فرضياتٍ يتم استنتاجها فورًا من الفرضيات السابقة عن طريق إحدى قواعد الاستدلال هذه. إذًا، يمكننا القول إنّ بالنسبة لراسل القضية (ج)، ومعها جميع القضايا التي طلبت السلحفاة إضافتها إلى لائحة الفرضيات أو المقدمات، لا يمكنها أن تُستعمَل بهذه الطريقة لأنها قواعد استدلالٍ يصدر عنها قضايا يمكن استعمالها كفرضياتٍ في حجةٍ معينةٍ. أي أنّ نتيجة القاعدة الاستدلالية يمكن أن تُستعمَل كفرضيةٍ أو مقدمةٍ لكن ليس القاعدة بذاتها. الفكرة الثانية لراسل هي التمييز بين القضية الشرطية (implication) والاستدلال (inference). القضية الافتراضية التي تكون بنيتها على شكل «إذا (ع) فإذًا (س)»، هي أحد أشكال القضية الشرطية، حيث تكون القضيتان (ع) و(س) غير مؤكّدةٍ، بمعنى أنها افتراضيةٌ[2]. أمّا الاستدلال الذي يكون على شكل «(ع) لذلك (س)» (A therefore B)، فتكون فيه (ع) و(س) مؤكدةً، بمعنى أنها ليست افتراضيةً. ويقول راسل أنّ بداية الحل لمفارقة لويس كارول هي الملاحظة بأنّ هناك التباس بين الاستدلال والقضية الشرطية (Russell, 35).
تابع الفيلسوف المعاصر ماثيو ماريون (Marion, 48-75)، وهو أستاذ فلسفة في جامعة كيبيك في مونتريال، مؤكّدًا أنّ بالنسبة لراسل، خطأ لويس كارول أنه في القضية الافتراضية الثانية (د) حصل اللغط بين القضية الشرطية والاستدلال. كما أوضح أنّ هذا اللغط كان يحصل بشكلٍ متواصلٍ منذ زمن الفلاسفة اليونانيون، حيث يؤكد أنّ أرسطو لم يستعمل الاستدلال إطلاقًا وإنما كان دائمًا يستعمل القضية الشرطية. إنّ القضية (د) هي على شكل ما سمّوه علماء المنطق في القرون الوسطى «القياس الاستثنائي» (Modus Ponens)، الذي يأتي على شكل «(ع) صادقةٌ، وإذا (ع) فإذًا (س)، لذلك (س) صادقةٌ». بما أنّ السلحفاة تقبل بصحّة (أ) و(ب)، فهي تضيف إليهما القضية الافتراضية «إذا (أ) و(ب) صادقتان فإذًا (ي) صادقةٌ» ومن المتوقع أن تستنتج أنّ (ي) صادقةٌ بالفعل، ولكنها لم تقبل بهذه النتيجة. حسب ماثيو ماريون، انطلاقًا من راسل، سبب الرفض هو اللغط بين «فإذًا» و«لذلك»، أي أنّ لويس كارول استعمل «لذلك» بذات الطريقة التي استعمل فيها «فإذًا»، ليس كاستدلالٍ منطقيٍّ لكن كقضيةٍ شرطيةٍ. حسب راسل، «فإذًا» تُستعمل بين قضيتين غير مؤكدتين، أمّا «لذلك» فتستعمل بين قضايا مؤكّدةٌ. كان استعمال لويس كارول للقضية (د) يعادل (equivalent) «(أ) و(ب) صادقتان، وإذا (أ) و(ب) صادقتان إذًا (ي) صادقةٌ، إذًا (ي) صادقةٌ»، والخطأ هو في ال-«إذًا» الثانية التي يجب أن تكون «لذلك» كوْن الفرضيات مؤكّدةٌ وليست افتراضيةً. فبالرغم من أنّ مضمون القضية «إذا (أ) و(ب) صادقتان إذًا (ي) صادقةٌ» افتراضيًا، لكن لويس كارول يستعملها كقضيةٍ مؤكّدةٍ بالنسبة للسلحفاة، غير مشروطةٍ ب-«إذا» أو «في حال» أو غيرها من التعابير الشَّرطية. ويعتبر ماريون أن القضية (د) يجب أن تكون «(أ) و(ب) صادقتان، و(ج) صادقةٌ، لذلك (ي) صادقة»، حيث (ج) هي القضية الافتراضية التي تتضمّن «إذًا» وليس «لذلك». الاختلاف الجذري بين الاستدلال والقضية الشرطية هو أنه حين نستعمل «لذلك» للاستدلال، علينا أن نقبل بالمبادئ غير المبرهنة وإلّا رفضنا أن يكون هناك ما يسمّى بعلم المنطق، وبمجرد أنّ السلحفاة طلبت من أخيل أن يقنعها «منطقيًا» بالقضية «ي»، فهي لم ترفض علم المنطق. إذًا، السلحفاة مرغمةٌ على قبول القضية (ي) في هذه الحالة.
كتب الفيلسوف البريطاني غلبرت رايل (1900 – 1976) مقالًا فلسفيًّا للتمييز بين «معرفة ذلك» و«معرفة كيف»، ذاكرًا بأنّ لويس كارول لم يميّز بينهما في روايته عن أخيل والسلحفاة (Ryle, 6). «معرفة ذلك» تمثّل تأكيدًا، واقعةً (fact)، أو فكرةً معينةً، كالقول بأنّ الضلع الأول يساوي الضلع الثاني في المثلث، إنها معلومةٌ تُضاف إلى معلوماتنا عن شيءٍ ما. أمّا «معرفة كيف»، أو المعرفة الكيفيّة، فهي معرفة الانتقال من معلومةٍ إلى أخرى، أي من «معرفة ذلك» إلى أخرى. يمكننا القول إنّ «معرفة كيف» هي قاعدةٌ (rule) تُصدِر معلوماتٍ معينةٍ. وتكمن أهمية هذا التمييز بأنه من الخطأ التعامل مع المعرفة الكيفية وكأنها مجرّد معلومةٍ. إنّ الخطأ الذي اقترفهُ أخيل أنه لم يعترض على استعمال السلحفاة للقضايا الافتراضية كأنها معلوماتٌ وهي في الحقيقة قواعدٌ. حسب تعبير غلبرت رايل، القضية الافتراضية «إذا (ع)، فإذًا (س)» هي «معرفة كيف» لأنها تعلّمنا كيف ننتقل من «معرفة ذلك»، أي معرفة (ع)، إلى «معرفة ذلك» أخرى، وهي (س). إنّ لويس كارول تعامَلَ مع كلّ قضيةٍ افتراضيةٍ أضافها إلى قائمة الفرضيات على أنها «معرفة ذلك»، وكان عليه أن يتعامل معها على أنها «معرفة كيف».
إذًا، انطلاقًا من رايل، يكون ماريون الذي استند على راسل مخطئًا بما فعله حين تعامل مع القضية الافتراضية كمعلومةٍ أو ك-«معرفة ذلك» في حين أنها «معرفة كيف». بالنسبة لماريون القضية (د) هي «(أ) و(ب) صادقتان، و(ج) صادقةٌ، لذلك (ي) صادقة». لكن علينا ملاحظة أن القضية (ج)، وهي «إذا كانت (أ) و(ب) صادقتين، فإذًا (ي) يجب أن تكون صادقةً»، هي قضيةٌ افتراضيةٌ تعلّمنا كيف ننتقل من فكرةٍ لأخرى. الفكرة الأولى هي «(أ) و(ب) صادقتان»، والثانية هي «(ي) صادقةٌ». إذًا معرفة (ج) بأنها صادقةٌ هي معرفةُ «قاعدةً» بأنها صادقةٌ، أو بالأحرى «معرفة كيف»، وليست «معرفة ذلك» لتكون عبارة عن معلومةٍ إضافيةٍ كما يستعملها ماريون، وكارول أيضًا، حين يضعها بجانب المعلومات الأخرى من دون تطبيقٍ، لتشكيل قضيةً افتراضيةً جديدةً.
(أ) معرفةٌ كيفيّةٌ
إنّ ما يهمّ الآن هي مسألة ما إذا كانت (أ) تُعتَبَر «معرفة كيف» أو «معرفة ذلك». القضية (أ) بتعبير إقليدس ولويس كارول هي «الأشياء التي تساوي الشيء ذاته تتساوى أيضًا مع بعضها بعضًا». فلنعتبر أن هذه الأشياء هي على سبيل المثال (س)، (ش)، و(ص)، وطبعًا مفهوم المساواة هنا يعني الكمية ذاتها ونعبّر عنه من خلال الرمز «=». إنّ القضية (أ) تعادل (equivalent) القضية الافتراضية «إذا (س)=(ص) و(ش)=(ص)، إذًا (س)=(ش)»، كما يمكنها أن تعادل القضية التالية: «إنّ (س)=(ص) و(ش)=(ص)، لذلك (س)=(ش)». في الحالتين سوف نصل للنتيجة ذاتها، وهي أنّ (أ) هي معرفةٌ كيفيّةٌ. هذا لأنّها تعلّمنا كيف ننتقل من فكرتين أو واقِعَتين إلى فكرةٍ أو واقِعَةٍ ثالثةٍ. «(س)=(ص)» هي الفكرة الأولى، وهي «معرفة ذلك»، وكذلك الأمر بالنسبة للفكرة الثانية «(ش)=(ص)»، والفكرة الثالثة «(س)=(ش)» التي هي النتيجة التي تعلّمُنا (أ) كيف ننتقل إليها. لذلك السبب يمكننا اعتبار (أ) قاعدةٌ تنقلنا من فكرةٍ لأخرى.
(أ) هي قاعدةٌ عامّةٌ ليست خاصةً بالمثلّثات مثلًا أو بأي شيءٍ معينٍ آخرٍ. ولكن لكي ننتقل من العام إلى الخاص علينا تطبيق القاعدة العامّة في حالاتٍ خاصةٍ. عندما نقبل بقاعدةٍ كحقيقةٍ، نقبلها بوصفها «معرفة كيف» وليس «معرفة ذلك»، أي أنه لا يمكننا قبولها نظريًّا ورفضها عمليًّا. إنّ قبول القاعدة يكون في تطبيقها في الحالات الخاصة، وهذا ما لم يفعله لويس كارول في المفارقة.
حلّ المفارقة
رأس الكلام في المفارقة يَكمُن في عدم تطبيق القضايا الافتراضية في حالاتٍ خاصةٍ، والسؤال الأساسي هو عن سبب عدم التطبيق هذا. إنّ الذي يمنع لويس كارول عن تطبيق القضايا الافتراضية هو اعتقاده أنّ قيمة الصّواب (truth value) لهذه القضايا، أي ما إذا كانت صادقةً أو غير صادقةٍ، هي مستقلةٌ عن قيمة الصّواب لقضاياها التي تتضمّنها. الاستقلالية هنا تعني أنه من الممكن أن تكون القضية (ع) صادقةً، وأن تكون القضية الافتراضية «إذا (ع) صادقةٌ فإذًا (س) صادقة» أيضًا صادقةٌ، لكن من دون أن تكون القضية (س) صادقةٌ. هذا هو السبب الأساسي لعدم تطبيق القضايا الافتراضية على المثلّث الذي تكلّم عنه إقليدس، وبالتالي يكون هذا سبب قيام المفارقة، كما أنه الخلاصة الجوهرية التي أراد لويس كارول أن يقدمها. لتسهيل الموضوع، فلنأخذ على سبيل المثال القياس الأرسطي التالي:
جميع البشر فانون (المقدمة الأولى)
سقراط بشريٌّ (المقدمة الثانية)
سقراط فانٍ (النتيجة)
الاستقلالية التي يعتمدها لويس كارول تعني أنه حتى لو كانت المقدمتان صادقتين والقضية الافتراضية «إذا كانت المقدمة الأولى والثانية صادقتين فإذًا النتيجة صادقةٌ» هي صادقةٌ، هذا لا يضمن أن تكون النتيجة صادقةً. إنّ ضمان النتيجة يتطلَّب تطبيق القضية الافتراضية، وترجمة هذا التطبيق يبدأ بتطبيق المقدمة الأولى العامة على المقدمة الثانية الخاصة بسقراط. وهذا ما يرفضه لويس كارول، والسبب هو أنه يأخذ الفرضية الأولى كـ«معرفة ذلك» بدلًا من «معرفة كيف». «جميع البشر فانون» تتضمّن فكرتين، الأولى هي فكرة البشرية والثانية هي فكرة الفناء. فهذه المقدمة تعادل «إذا كنت بشرًا، فإذًا أنت فانٍ» أو «إننا بشرٌ، لذلك نحن فانون». فالاستنتاج بأنّ سقراط هو فانٍ انطلاقًا من أنه بشريٌ يدلّ أننا نستعمل القضية الأولى بهذا الشكل. إنّ القضية الأولى تعلّمنا الانتقال من مفهوم البشر إلى مفهوم الفناء، لذلك هي قاعدةٌ، بمعنى أنها معرفةٌ كيفيةٌ، يتطلّب قبولها كحقيقةٍ، أو كقضيةٍ صادقةٍ، تطبيقًا لها في الحالات الخاصّة.
الآن، فلنعد إلى مفارقة السلحفاة. إذًا، القضية (أ) هي قاعدةٌ عامّةٌ، أمّا القضايا (ب) و(ي) هي معلوماتٌ عن مثلثٍ معينٍ، أي حالةٍ خاصّةٍ. إنّ السلحفاة تعتبر أنّ القضية (أ) صادقةٌ، لذلك على أخيل أن يطلب منها تطبيقها على المثلث الذي رسمه إقليدس. (أ) تعادل «إنّ (س)=(ص) و(ش)=(ص)، لذلك (س)=(ش)»، والتطبيق يبدأ بأن نعتبر الضلع الأول من المثلث هو (س)، الضلع الثاني هو (ش)، والضلع الثالث هو (ص). وبما أنّ السلحفاة تعتبر القضية (ب) صادقةٌ، أي أنّ ضلعا هذا المثلث هما شيئان مساويان لشيءٍ ثالثٍ، والشيء الثالث هنا هو الضلع الثالث (ص)، فهي مرغمةٌ على قبول أن الضلعين متساويان، أي أنّ (ي) صادقةٌ.
وفي حال أرادت السلحفاة تشكيل القضية الافتراضية (ج)، فعلى أخيل أن يرفض استعمال القضية (أ) فيها كمعلومةٍ، أي «معرفة ذلك». فحتى إن وضعنا القاعدة (أ) كمقدمةٍ، علينا استعمالها كقاعدةٍ. إذًا، يمكن للسلحفاة القول إنّه مع العلم أن القاعدة (أ) صادقةٌ ويمكننا تطبيقها، من الضرورة أن تكون (ج) صادقةٌ، و(ج) هي «إذا كانت (ب) صادقةً، فإذًا (ي) صادقةٌ». لكن على أخيل أن ينبّه السلحفاة أنّ (ج) هي أيضًا قاعدةٌ تنقلنا من فكرةٍ إلى أخرى ويجب تطبيقها ما دام أننا قبلنا بحقيقتها بعد تدوينها بين المقدمات أو الفرضيات. لذلك، وبما أنّ السلحفاة تعتبر القضية (ب) صادقةٌ، أي أن ضلعا هذا المثلث هما شيئان مساويان لشيءٍ ثالثٍ، والشيء الثالث هنا هو الضلع الثالث (ص)، فتطبيق القاعدة يوصلنا إلى (ي)؛ أنّ الضلعين متساويان.
الخاتمة
إنّ لانهائية الفرضيات تأتي من عدم تطبيق القواعد ومن التعامل مع هذه القواعد على أنها معلوماتٌ أو وقائعٌ يمكن وضعها داخل القضايا الافتراضية. لذلك، كان الحلّ بالتمييز بين «معرفة ذلك» التي يمكن استعمالها كواقعةٍ داخل القضايا الافتراضية والقواعد، وبين المعرفة الكيفية التي لا يجب أن تُستعمَل كمعلومةٍ في القواعد لأنها قاعدةٌ بحدّ ذاتها، وقبول حقيقتها يعني قبول تطبيقها في الحالات الخاصة.
——————————————-
[1] يمكن تسميتها أيضًا مقدّمات (premises).
[2] القضية الافتراضية هي التي تُستعمَل بما معناه «في حال كانت صادقةً» عادةً تأتي ضمن الشكل الافتراضي «إذا (أ) فإذًا (ب)»، أمّا القضية المؤكدة تُستعمَل من دون الشكل الشرطي في القضية، مع العلم أن هذا الاستعمال لا يعني أنها صادقةٌ أو كاذبةٌ.
References:
Carroll, Lewis. “what the Tortoise Said to Achilles.” Mind 104, no. 416 (1995): 691-693.
(Euclid) J.L. Heiberg. Euclid’s Elements of Geometry. Richard Fitzpatrick (2008). (ISBN 978-0-6151-7984-1).
Marion, Mathieu (2016). Lessons from Lewis Carroll’s Paradox of Inference. The Carrollian. The Lewis Carroll Journal, (28), 48–75.
Russell, Bertrand. The Principles of Mathematics. Forgotten Books. 2014.
Ryle, Gilbert. “I.—Knowing how and Knowing that: The Presidential Address.” Proceedings of the Aristotelian Society 46, no. 1 (1946): 1-16.
